Dimensionality Reduction Algorithms in Biology: UMAP, t-SNE, PCA, and Beyond

Introduction

In the era of big data, biologists often find themselves grappling with datasets of staggering complexity. From gene expression profiles to protein structures, the high-dimensional nature of biological data presents both opportunities and challenges. Enter dimensionality reduction algorithms – powerful tools that help scientists navigate this complexity by distilling the essence of high-dimensional data into more manageable, lower-dimensional representations.

In this blog post, we'll explore three popular dimensionality reduction techniques – UMAP, t-SNE, and PCA – and discuss their applications in biology. We'll also touch on how these methods relate to Neruosnap services like ClusterProt, which is a method for clustering proteins based on the structure similarity.

Understanding Dimensionality Reduction

Schematics of Dimensionality Reduction, taken from https://www.sc-best-practices.org/

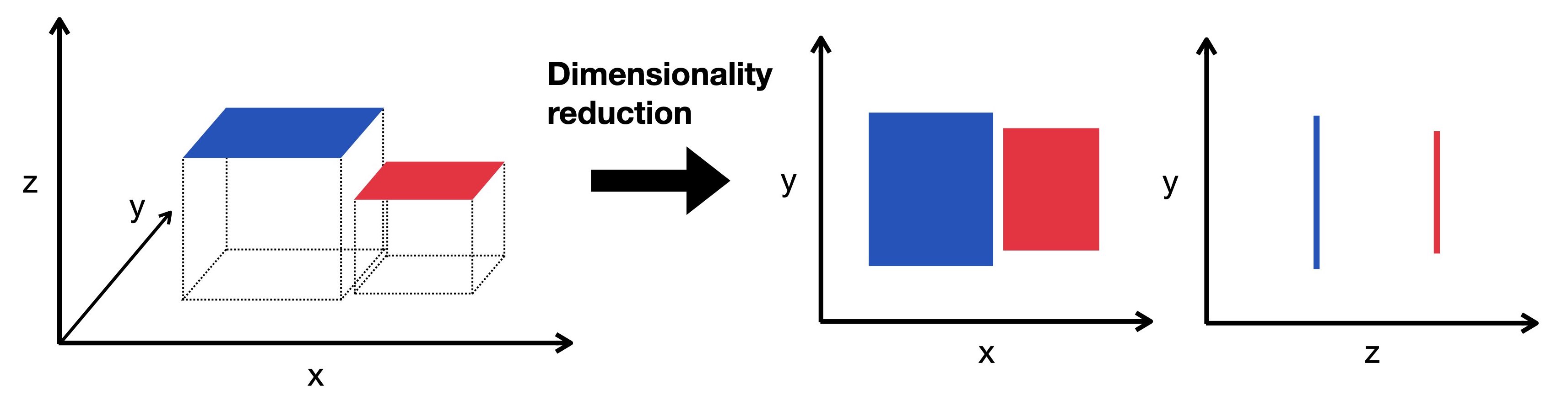
Before diving into specific algorithms, let's clarify what we mean by dimensionality reduction. In essence, it's a set of techniques used to reduce the number of features in a dataset while retaining as much important information as possible. This process helps in:

1. Visualization: Mapping high-dimensional data to 2D or 3D space for visual analysis.
2. Noise reduction: Eliminating less important features that might be noise.
3. Computational efficiency: Reducing the computational resources needed for analysis.

Now, let's examine three popular dimensionality reduction algorithms:

Principal Component Analysis (PCA)

PCA is one of the oldest and most widely used dimensionality reduction techniques. It works by identifying the principal components – directions in the data that account for the most variance.

How PCA works

1. Standardize the data
2. Compute the covariance matrix
3. Calculate eigenvectors and eigenvalues
4. Sort eigenvectors by decreasing eigenvalues
5. Choose top k eigenvectors as the new features

One of the advantages of this approach is that it is fast and simple to implement, making it accessible for many applications. It also has the benefit of preserving the global structure of data, which can be particularly useful when dealing with linear relationships. However, a key limitation is that it assumes linearity, which may cause it to overlook important non-linear patterns in the data, reducing its effectiveness in more complex scenarios.

t-Distributed Stochastic Neighbor Embedding (t-SNE)

t-SNE is a nonlinear technique that's particularly good at preserving local structures in the data.

How t-SNE works

1. Compute pairwise similarities in high-dimensional space
2. Create a probability distribution over pairs of data points
3. Create a similar distribution in low-dimensional space
4. Minimize the difference between these distributions

This method excels at preserving local structure and can effectively reveal clusters within the data, making it useful for uncovering underlying patterns. However, it comes with the drawback of being computationally intensive, which can make it less practical for large datasets. Additionally, its results can be sensitive to the choice of hyperparameters, requiring careful tuning to achieve optimal outcomes.

Uniform Manifold Approximation and Projection (UMAP)

UMAP is a more recent algorithm that aims to preserve both local and global structure.

How UMAP works

1. Construct a weighted graph representing the data
2. Create a low-dimensional representation of this graph
3. Optimize the low-dimensional representation to be as close as possible to the high-dimensional one

This approach offers the advantage of being faster than t-SNE while also preserving both local and global structure, making it more suitable for larger datasets. UMAP also benefits from having more understandable and interpretable parameters compared to t-SNE, easing its tuning process. However, it still shares the limitation of being sensitive to hyperparameters, which can affect the quality of the results. Additionally, it tends to be less intuitive than PCA, which may complicate its interpretation.

Comparison in Biological Contexts

Dimensionality reduction techniques such as PCA, t-SNE, and UMAP are critical in addressing the challenges of high-dimensional biological data, particularly in genomics, proteomics, and single-cell analysis. In genomic studies, PCA has been widely used to reduce complex datasets while retaining key biological signals, such as identifying genetic variations linked to specific diseases. t-SNE, meanwhile, has proven particularly useful in single-cell RNA sequencing (scRNA-seq) by revealing hidden cell subpopulations, as it excels at distinguishing subtle differences between closely related cell types. This has enabled breakthroughs in understanding cell differentiation and disease progression. UMAP, increasingly favored over t-SNE for large datasets, has enhanced the analysis of complex tissues by providing faster computation and clearer visualization of cellular hierarchies. In multi-omics studies, UMAP has facilitated integrative analyses by preserving both local and global data structure, enabling deeper insights into cross-omics relationships. Collectively, these methods have transformed the ability to analyze, visualize, and interpret large-scale biological datasets, driving discoveries in disease research and personalized medicine.

ClusterProt Service: Cluster proteins based on structure similarity

ClusterProt is a service that clusters protein structures based on their structural similarity. It leverages dimensionality reduction techniques to transform high-dimensional protein structure data into lower-dimensional projections, making it easier to group similar conformations.

This approach simplifies complex protein data, enabling researchers to identify structural patterns and relationships between different conformational states or protein variants. By reducing the dimensionality of protein structures, ClusterProt allows for more efficient visualization and analysis of clusters, facilitating deeper insights into protein dynamics.

Conclusion

Dimensionality reduction techniques like PCA, t-SNE, and UMAP have become essential tools in biological data analysis. Each method offers unique advantages: PCA for global structure and linear relationships, t-SNE for preserving local structures in single-cell analysis, and UMAP for balancing local and global preservation in large-scale studies.

These techniques extend beyond visualization, playing crucial roles in disease research, drug discovery, and personalized medicine. Services like ClusterProt demonstrate their practical applications in areas such as protein structure analysis.

As biological datasets continue to grow, understanding and effectively using these dimensionality reduction methods will be key to extracting meaningful insights and advancing our understanding of biological systems.

Read More

For further exploration of dimensionality reduction techniques and their applications in biology, consider the following resources:

1. https://arxiv.org/abs/1802.03426
2. https://lvdmaaten.github.io/publications/papers/JMLR_2008.pdf
3. https://www.cs.cmu.edu/~elaw/papers/pca.pdf
4. https://distill.pub/2016/misread-tsne/
5. https://www.sc-best-practices.org/preprocessing_visualization/dimensionality_reduction.html