Protein Symmetries Simplified. Understanding Cn, Dn, and Cubic Symmetries.
Written by Keaun Amani | Published 2024-7-8
Written by Keaun Amani | Published 2024-7-8
In this mini tutorial we're going to cover the basics of protein symmetries and how they can be used to design and predict structures of more advanced multimers and complexes. Protein symmetries, refer to the ways in which a protein's structure can be rotated around an axis and still appear identical after a full rotation. These symmetries are a fundamental aspect of protein structure and function, and understanding them is crucial in fields like biochemistry and structural biology.
Furthermore, a strong understanding of these symmetries is valuable when it comes to utilizing certain tools and models like RoseTTAFold2 and RFdiffusion on Neurosnap.
While there are many different types of protein symmetries, the one's we are going to cover in this blog post consist of Unspecified / No Symmetry, Cyclic (Cn), Dihedral (Dn), and Cubic symmetries. Cubic symmetries can then be broken down into other symmetries like Tetrahedral (T), Octahedral (O), and Icosahedral (I).
Additionally, it is noteworthy to learn that the number that directly follows the letter of a symmetry indicates the order of the complex. This is a bit tricky as the number of chains are not equal to the order of a complex, which is more like the number of symmetric units within the complex. For example consider the following for cubic symmetries:
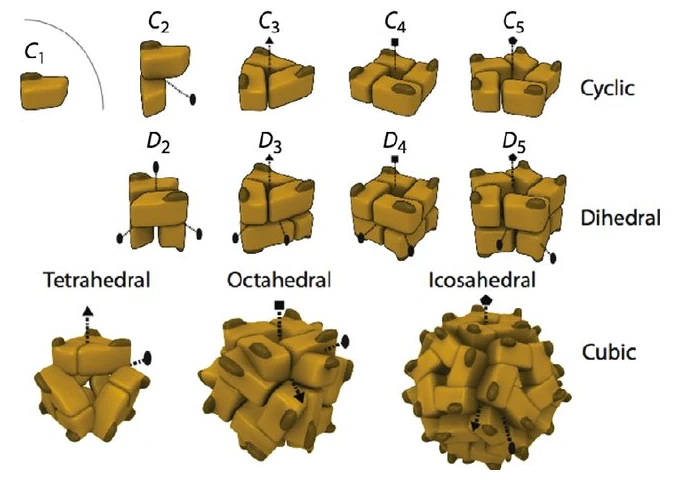
As the name entails, unspecified symmetries are complexes without any particular symmetry. This can include hetero-dimers as well as arguably the vast majority other naturally forming multimers. This is sometimes denoted with "X" though this varies.
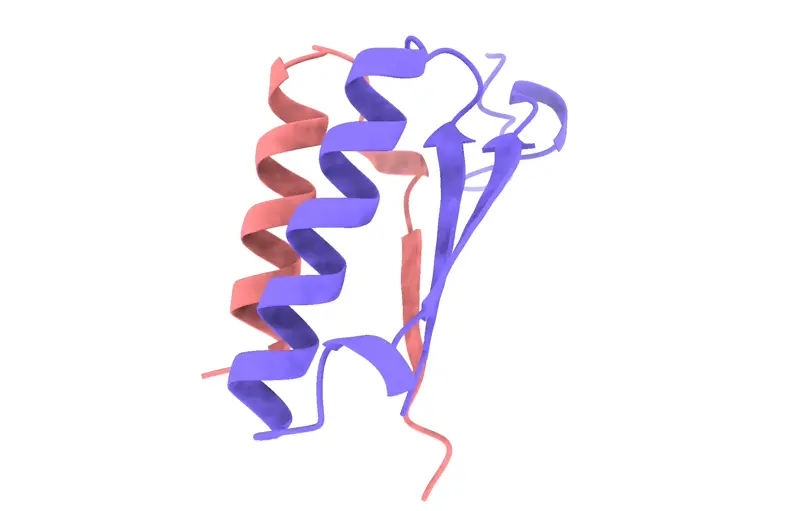
The "C" in C2, C3, etc., stands for "cyclic." The number that follows indicates the number of rotations needed for the protein to look the same as its original position. This is also known as the order of symmetry. C2 Symmetry: A protein with C2 symmetry has a twofold rotational symmetry. This means that the protein can be rotated 180 degrees (360°/2) around an axis and its structure will appear identical to its original orientation. Essentially, it looks the same twice in a 360-degree rotation.
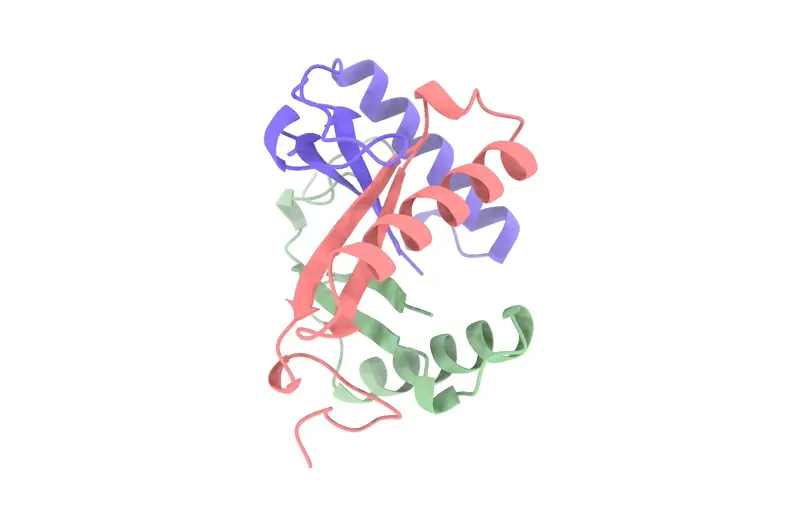
C3 Symmetry: A protein with C3 symmetry has a threefold rotational symmetry. Here, the protein can be rotated 120 degrees (360°/3) around an axis and it will look the same. In a full 360-degree rotation, the protein's structure will align with its original orientation three times.
Higher Order Symmetries (C4, C5, etc.): Similarly, C4 symmetry means the protein has a fourfold symmetry (90-degree rotation), C5 symmetry means a fivefold symmetry (72-degree rotation), and so on. The higher the symmetry order, the more times the protein will look identical during a full 360-degree rotation around the symmetry axis.
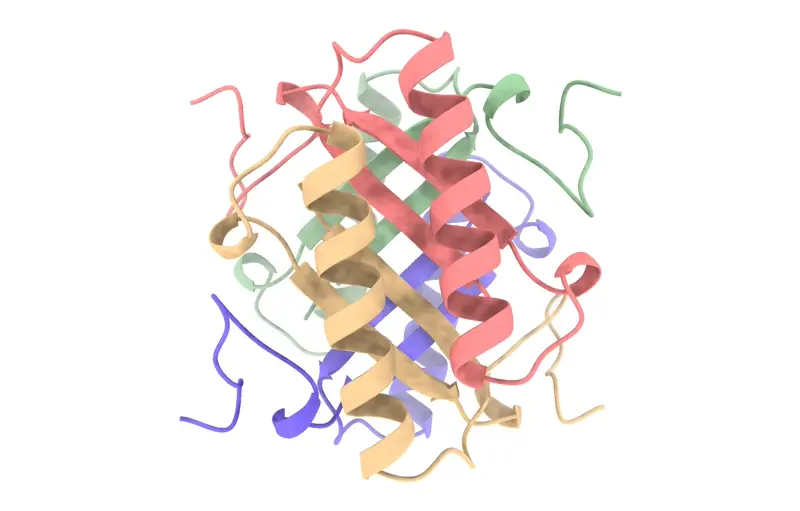
Dihedral symmetry in proteins, denoted as Dn, is characterized by the presence of not just one, but two types of rotational symmetry axes. In these structures, a primary cyclic symmetry axis (Cn) is accompanied by multiple secondary axes, which are perpendicular to the primary axis. The number following the 'D' (as in D2, D3, etc.) represents the order of the primary cyclic symmetry.
D2 Symmetry: For instance, in a protein with D2 symmetry, there are two secondary axes, each associated with twofold symmetry (C2), along with the primary axis of twofold symmetry. This setup creates a symmetry where the protein looks the same four times during a 360-degree rotation.
D3 Symmetry: A D3 symmetric protein has a primary axis of threefold symmetry (C3) and three secondary axes of twofold symmetry (C2). This complex symmetry leads to a structure that repeats its orientation multiple times within a full rotation.
Higher Order Dihedral Symmetries: In higher-order dihedral symmetries like D4, D5, etc., the complexity increases with more secondary axes intersecting the primary axis, leading to intricate and repetitive structural patterns in proteins.
Tetrahedral symmetry, denoted as T, is a type of cubic symmetry seen in some protein complexes. In these structures, four threefold axes of rotational symmetry intersect at the corners of a tetrahedron. Additionally, there are three twofold axes of symmetry that intersect at the edges of the tetrahedron. This unique arrangement results in a highly symmetrical structure that is vital in understanding the organization of certain viral capsids and other complex molecular assemblies.
Octahedral symmetry, indicated by 'O', is another form of cubic symmetry where the axes of symmetry align with the vertices and faces of an octahedron. In this arrangement, there are three fourfold axes, four threefold axes, and six twofold axes. This type of symmetry is less common than tetrahedral symmetry but is critical in the assembly of some large protein complexes, offering a robust and symmetrical framework for their structural organization.
Icosahedral symmetry, represented as 'I', is one of the most complex forms of protein symmetry. It involves twenty triangles forming a nearly spherical shape, resembling a soccer ball. This form of symmetry incorporates six fivefold axes, ten threefold axes, and fifteen twofold axes. Icosahedral symmetry is particularly significant in the study of virus capsids, where it is utilized to pack genetic material efficiently within a compact and stable structure.

Understanding these protein symmetries is essential in several areas of structural biology and bioinformatics. For instance, in the design of novel protein structures using tools like RoseTTAFold2 and RFdiffusion on Neurosnap, knowledge of symmetries helps in accurately predicting the folding and assembly of proteins. Additionally, in the study of viral capsids and other large protein complexes, recognizing the type of symmetry can provide insights into their stability, assembly mechanism, and function.
In conclusion, a comprehensive grasp of protein symmetries not only aids in the theoretical understanding of protein structures but also has practical implications in fields ranging from drug design to the development of nano-materials. As we continue to explore the vast world of proteins, the role of symmetry in understanding and manipulating these biological macromolecules becomes increasingly apparent.
By Danial Gharaie Amirabadi
By Danial Gharaie Amirabadi
By Danial Gharaie Amirabadi
By Keaun Amani
By Keaun Amani
By Keaun Amani
Register for free — upgrade anytime.
Interested in getting a license? Contact Sales.
Sign up free